


Next: Simulation Results
Up: MAP Sequence Estimation for
Previous: First Order Gauss Markov
In this Section we summarize the development of the MLSE algorithm for a fast
fading Gauss-Markov channel model.
Given prior information on the sequence distribution, the corresponding MAP
estimator is a straightforward extension (e.g. [14]).
For the Gauss Markov model under consideration here,
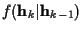 is Gaussian with mean
is Gaussian with mean
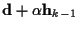 and covariance
and covariance 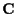 .
.
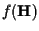 can be written as
can be written as
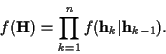 |
(6) |
To simplify expressions, we assume below that 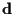 is zero.
We also assume that the initial channel coefficient
vector
is zero.
We also assume that the initial channel coefficient
vector  is known (e.g. estimated from a previous data
block). Substituting (2) and (6)
into (4), we obtain
is known (e.g. estimated from a previous data
block). Substituting (2) and (6)
into (4), we obtain
We can marginalize over the channel coefficient distribution, integrating step
by step as shown in [8].
After the integration over all of the channel coefficients, we have the
likelihood function
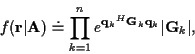 |
(8) |
where the 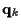 and
and 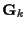 ;
;
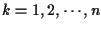 are given as
are given as
and
If we take the negative natural logarithm of (8), we will
obtain the time-recursive form of the cost function:
![\begin{displaymath}- \log f({\bf r}\vert{\bf A}) \doteq
- \sum_{k=1}^n \left[{{...
..._k}^{H} {\bf G}_k {\bf q}_k}+\log \vert{\bf G}_k\vert
\right].
\end{displaymath}](img71.gif) |
(12) |
From the expressions for 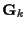 and
and 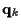 ,
we see that the
transition costs of the Viterbi algorithm
depend on all of the previous states. So the standard Viterbi
algorithm can not be optimally applied here. Optimum results can be obtained
by exhaustive search. Alternatively,
computationally feasible suboptimum algorithms can
be considered. Here we describe a suboptimum algorithm which employs
the generalized Viterbi algorithm (GVA) [10]
to prune possible data sequences. Considering a trellis formulation,
at each state of each stage we keep
,
we see that the
transition costs of the Viterbi algorithm
depend on all of the previous states. So the standard Viterbi
algorithm can not be optimally applied here. Optimum results can be obtained
by exhaustive search. Alternatively,
computationally feasible suboptimum algorithms can
be considered. Here we describe a suboptimum algorithm which employs
the generalized Viterbi algorithm (GVA) [10]
to prune possible data sequences. Considering a trellis formulation,
at each state of each stage we keep
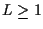 survivor paths (i.e. surviving hypothesized sequences).
For each survivor, the
survivor paths (i.e. surviving hypothesized sequences).
For each survivor, the 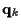 and
and 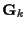 required for the incremental cost are computed.
(Since for each survivor path the
required for the incremental cost are computed.
(Since for each survivor path the 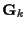 and
and 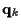 are computed
from the sequence associated with that path, we can interpret this as
data-aided estimation of the incremental cost corresponding to the particular
path, so this algorithm is effectively a form of PSP [9].)
At time n the sequence estimate corresponds to the best surviving path.
As L increases, the PSP algorithm results will approach the optimum.
Simulations in [8] show that this approach results in effective
algorithms for ML (or MAP) sequence estimation over unknown, fast time-varying
channels for reasonably small values of L. We have found that
are computed
from the sequence associated with that path, we can interpret this as
data-aided estimation of the incremental cost corresponding to the particular
path, so this algorithm is effectively a form of PSP [9].)
At time n the sequence estimate corresponds to the best surviving path.
As L increases, the PSP algorithm results will approach the optimum.
Simulations in [8] show that this approach results in effective
algorithms for ML (or MAP) sequence estimation over unknown, fast time-varying
channels for reasonably small values of L. We have found that 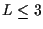 is typically adequate.
is typically adequate.



Next: Simulation Results
Up: MAP Sequence Estimation for
Previous: First Order Gauss Markov
Rick Perry
2001-03-19
![]() is Gaussian with mean
is Gaussian with mean
![]() and covariance
and covariance ![]() .
.
![]() can be written as
can be written as