


Next: Illustrative Numerical Examples
Up: Trellis Structure Approach to
Previous: Trellis Diagram Formulation
Based on the trellis diagram problem formulation described above, we now
describe a multitarget track estimation algorithm which provides a list of
L best K-tracks as well as estimates of the number of tracks. The
algorithm is sequential, self-initiating and can handle false alarms and
missed detections. In this section a K-track algorithm is described, so
that K=1 is treated within this context.
The Bayesian tracking problem described in Section 3 would, if solved
directly, be computationally prohibitive for large n and even moderate
values of K and the Jm 's. Here we propose to reduce or prune the
number of candidate tracks by effectively, at each time m, eliminating
from further consideration the candidate tracks that have too large
(i.e. too unlikely) total costs at that time. In the trellis problem
formulation, this will be implemented by only keeping the L best sets of
tracks into each state.
The problem is to find the lowest cost path through the trellis. The
Viterbi algorithm [7] can be used to sequentially prune the paths
through the trellis for certain ML optimization problems (as well as for
some other problems). At any stage in the trellis, it keeps only one path
to each state. So it is only applicable to problems for which all other
paths can not be optimum. It has been used extensively in digital
communication and other application problems for which the sequence can be
modeled as a Markov process. It has also been proposed for multitarget
tracking based on a deterministic energy cost [6], where the
incremental path costs from a state
jm-1 (l) to a state jm (l) is a
function of only the
jm-1 (l) and jm (l) measurements.
In general, multitarget tracking problems, couched in a trellis framework,
can not be solved using the Viterbi algorithm. For the Bayesian estimation
problem considered here, the need for (infinite memory) Kalman filters for
each candidate track precludes its use, so that to solve the problem at
time n an exhaustive search of all In' paths through the trellis
appears necessary. At any stage n in the trellis, this requires that we
consider all paths into each state at stage n-1, each extended to all
states at stage n. That is, the
In-1' paths into stage n-1 must
be extended to the In' paths into stage n, even though the costs
of some of these paths will indicate that the corresponding K-track sets
are highly unlikely. Alternatively, we propose to keep, at each stage in
the trellis, a ``list'' of only the best (lowest cost) L paths to each
state, where L is selected to assure that no feasible paths are pruned
4.
Generically, the list Viterbi algorithm [8] does this. The
multitarget tracking algorithm we propose incorporates the list Viterbi
algorithm, along with the K-track trellis formulation of the multitarget
tracking problem [6], and Bayesian cost computation based on Kalman
filter innovations from Section 3. The algorithm determines a list of Lfeasible K-tracks sets as a list of L paths through the trellis. In
general, paths are evaluated according to a defined cost function, where
the incremental costs in progressing from stage to stage are computed as
branch costs from states to states.
Algorithm
- 1)
- Setup:
For each time
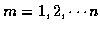 ,
allocate arrays of size Mm-by-L for the
predecessor state indices, predecessor state L-best indices,
permutation number of the current state measurement indices to track
associations, and current total minimum negative log costs. Allocate
Kalman filters for each track in each L-best sets of tracks for each state.
,
allocate arrays of size Mm-by-L for the
predecessor state indices, predecessor state L-best indices,
permutation number of the current state measurement indices to track
associations, and current total minimum negative log costs. Allocate
Kalman filters for each track in each L-best sets of tracks for each state.
- 2)
- Initialization:
For
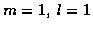 ,
the current costs are set using
(17) for the apriori
probabilities, since no Kalman filter innovations are available
initially. The Kalman filters are initialized using the available
measurements for time m=1, and using predicted values for time m=2.
,
the current costs are set using
(17) for the apriori
probabilities, since no Kalman filter innovations are available
initially. The Kalman filters are initialized using the available
measurements for time m=1, and using predicted values for time m=2.
- 3)
- Iteration:
For each time
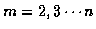 ,
and for each state
,
and for each state
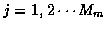
- 3.1)
- Add incremental costs (16)
from the L-best of each previous state to the total previous costs, and
temporarily store these candidate new costs.
- 3.2)
- Select the L-best of the candidate new costs and update the
associated Kalman filters.
- 4)
- Results:
- 4.1)
- Output the final L-best sets of tracks.
- 4.2)
- Output estimates of
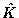 ,
using just the
lowest cost results for a joint estimation (21), or
marginalization over the L-best tracks as an approximation to
(22).
,
using just the
lowest cost results for a joint estimation (21), or
marginalization over the L-best tracks as an approximation to
(22).
The algorithm uses a fixed value of K, and can extract k-track sets from
the L-best K-track results for
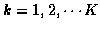 .
.
Although the algorithm is described above in block form, it is time-recursive,
and at any time during the iterations can produce current estimates of the
L-best tracks and 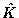 .
As usual with the Viterbi algorithm, the
trellis can be truncated periodically, to limit storage to a fixed size.
.
As usual with the Viterbi algorithm, the
trellis can be truncated periodically, to limit storage to a fixed size.



Next: Illustrative Numerical Examples
Up: Trellis Structure Approach to
Previous: Trellis Diagram Formulation
Rick Perry
1999-03-10
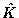 ,
using just the
lowest cost results for a joint estimation (21), or
marginalization over the L-best tracks as an approximation to
(22).
,
using just the
lowest cost results for a joint estimation (21), or
marginalization over the L-best tracks as an approximation to
(22).