


Next: Discussion
Up: EM Algorithms for Source
Previous: Temporally Independent Signal Amplitudes
Gauss-Markov Signal Amplitudes
For a Gauss-Markov time-varying signal amplitude vector,
let 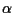 represent a complex first-order Markov factor.
Let the signal amplitude vector follow a
Gauss-Markov distribution such that, at time k:
represent a complex first-order Markov factor.
Let the signal amplitude vector follow a
Gauss-Markov distribution such that, at time k:
 |
(22) |
where  is complex, white, and Gaussian
with mean
is complex, white, and Gaussian
with mean 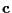 and covariance
and covariance 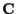 .
In this case,
.
In this case,
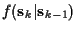 is Gaussian with mean
is Gaussian with mean
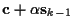 and covariance
and covariance 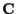 .
The
.
The
 from (12) with the
from (12) with the
 and
and  from (13,14) still apply.
from (13,14) still apply.
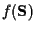 can be written as:
can be written as:
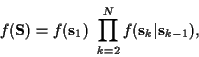 |
(23) |
so from (10) and (3)
 becomes:
becomes:
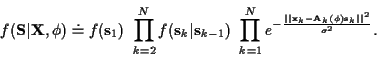 |
(24) |
To determine
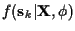 ,
and thereby
,
and thereby  and
and  ,
we must integrate
(24) over
,
we must integrate
(24) over
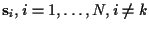 .
Due to space limitations, the derivation of this integration result is
not shown here. A parallel derivation for a similar model and problem
(a Gauss-Markov FIR intersymbol interference channel model for a
digital communication problem) appears in [10].
The result is that
.
Due to space limitations, the derivation of this integration result is
not shown here. A parallel derivation for a similar model and problem
(a Gauss-Markov FIR intersymbol interference channel model for a
digital communication problem) appears in [10].
The result is that
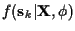 is Gaussian,
with mean
is Gaussian,
with mean  and covariance
and covariance  determined in the E-step
by the following recursive algorithm:
determined in the E-step
by the following recursive algorithm:
1) Initialize: for

2) Iterate: for

 and
and  from above
will be used in
from above
will be used in
 for the M-step
cost function for time k.
for the M-step
cost function for time k.
3) Update for the next EM iteration:
with
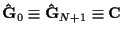 ,
,
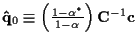 ,
and
,
and
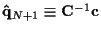 .
It is apparent from the above algorithm that
.
It is apparent from the above algorithm that
 at any time k depends on
all of the received data and estimated symbols from time 1 to N.
at any time k depends on
all of the received data and estimated symbols from time 1 to N.
The detailed EM algorithm for Gauss-Markov 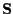 is:
is:
- 1.
- Initialize
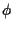 to an estimate of
to an estimate of
 .
.
- 2.
- E-step: use the algorithm from (25-27)
to estimate
 and
and  ,
,
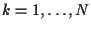 .
.
- 3.
- M-step: use the cost function (12) to estimate
 .
.
- 4.
- Set
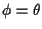 and repeat steps 2 and 3 until
converged.
and repeat steps 2 and 3 until
converged.
To initialize 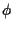 in step 1,
we could, for example, initialize
in step 1,
we could, for example, initialize  and
and  using
using
 in (25-27).
in (25-27).



Next: Discussion
Up: EM Algorithms for Source
Previous: Temporally Independent Signal Amplitudes
Rick Perry
2000-03-16