Next: Gauss-Markov Signal Amplitudes
Up: EM Algorithms for Source
Previous: EM Algorithms for Source
If the signal amplitude vectors 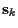 are independent over time,
then
are independent over time,
then
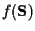 can be written as:
can be written as:
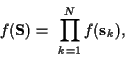 |
(15) |
and
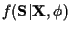 becomes:
becomes:
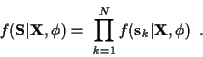 |
(16) |
From (10) and (3) we have that
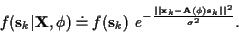 |
(17) |
For temporally independent Gaussian signal amplitudes,
let
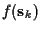 be a joint Gaussian distribution with
mean
be a joint Gaussian distribution with
mean 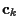 and covariance
and covariance 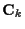 :
:
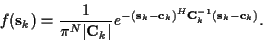 |
(18) |
In this case (17) specifically becomes
with
To initialize 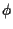 in step 1, we could, for example, initialize
in step 1, we could, for example, initialize
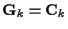 and
and
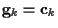 ,
,
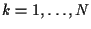 .
.



Next: Gauss-Markov Signal Amplitudes
Up: EM Algorithms for Source
Previous: EM Algorithms for Source
Rick Perry
2000-03-16